Basic Statistics with R

Chi-square distribution

While studying the gamma distribution in the previous section, we learnt the expression for its probability distribution function(PDF) to be

\(~~~~~~~~~~~~~~~~\small {f(x) = \dfrac{1}{\Gamma(\alpha) \theta^\alpha} {\large x}^{\alpha-1}{\large e}^{-x/\theta},~~~~~~~~~~~0 \leq x \lt \infty }\)

where \(\small{\theta}\) is the waiting time until the first event, and \(\small{\alpha}\) is the number of events for which we are waiting to occur in a Poisson process.



Let us consider a special case of the gamma distribution with \(\small{\theta = 2}\) and \(\small{\alpha = \dfrac{r}{2}}\). Substituting these values into the above formula, we get a new PDF given by,

\(~~~~~~~~~~~~~~~~\small {F(x) = \dfrac{1}{\Gamma(r/2) 2^{r/2}} {\large x}^{r/2 - 1}{\large e}^{-x/2},~~~~~~~~~~~0 \leq x \lt \infty }\)

This new function F(x) is called the Chi-square distribution with r degrees of freedom , and is an important function in the statistical analysis. (We will soon learn about the meaning of "degrees of freedom" as we go along). This is generally represented by a symbol \(\small{\chi^2(1)}\). Therefore, the expression for the PDF of a Chi-square distribution with r dgrees of freedom is written as,


\(~~~~~~~~~~~~~~~~\small {\chi^2(x,r) = \dfrac{1}{\Gamma(r/2) 2^{r/2}} {\large x}^{r/2 - 1}{\large e}^{-x/2},~~~~~~~~~~~0 \leq x \lt \infty }\)






The mean and variance of the Chi-square distribution are given by,

\(~~~~~~~~~~~~~~~~~\small{mean = \mu = \alpha \theta = (\dfrac{r}{2})r~ =~ r }\)
\(~~~~~~~~~~~~~~~~~\small{variance = \sigma^2 = \alpha \theta^2 = (\dfrac{r}{2}) 2^2 ~=~ 2r }\)









Thus, for a chi-square distribution, the mean equals the number of degrees of freedom and the variance equals the twice the number of dgrees of freedom .



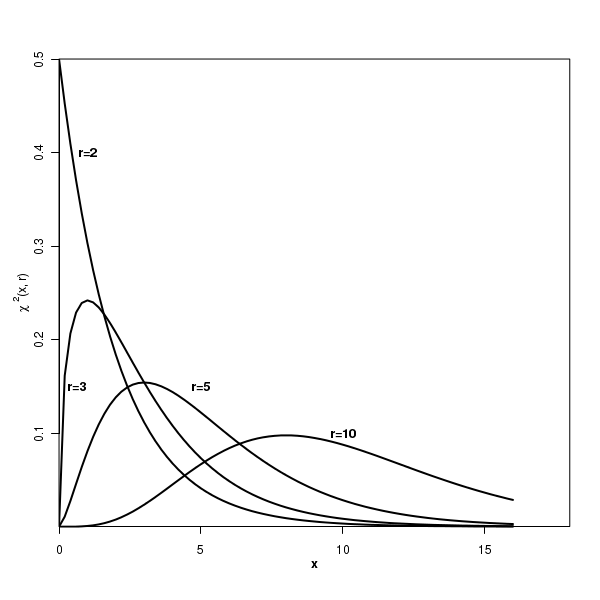
The plot of the Chi-square distribution

Before we understand the importance of the chi-square distribution, let us look at the plot of its PDF for various valus of the degrees of freedom:



Important properties of Chi-square distribution


Some important properties of the chi-square distribution used in statistical analysis are stated here in the form of theorems,

\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) Theorem 1

For a random variable X following normal distribution \(\small{N(\mu, \sigma)}\), the square of the variable \(\small{Z = \dfrac{X-\mu}{\sigma}}\) follows \(\sigma^2 \chi^2(X,1) \)

As a special case of this, for a random variable X following unit normal distribution \(\small{N(0, 1)}\), the square of the variable \(\small{Z = \dfrac{X-\mu}{\sigma}}\) follows a Chi-square distribution with one degree of freedom. ie.,
\(~~~~~~~~~~~~~~~~\small{~\ Z^2 = (\dfrac{X-\mu}{\sigma})^2 \rightarrow \chi^2(X,1) } \)

\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) Theorem 2

If the variables \(\small{Z_1, Z_2, Z_3,....,Z_n}\) have standard normal distributions \(\small{N(0,1)}\), then their sum \(~~~~~~~~~~~~~~~~\)

\(\small{W = Z_1^2 + Z_2^2 + Z_3^2 + .... + Z_n^2}~~~~\) follows \(\small{\chi^2(n)}\) distribution.

\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) Theorem 3

Let \(\small{X_1, X_2, X_3,....,X_n}\) be random samples of size n from a noraml distribution \(\small{N(\mu, \sigma) }\). From this data, we can estimate the samples mean and sample variance using,
$$ \small{\overline{X} = \dfrac{1}{n} \sum_{i=1}^n X_i}~~~~~~~~and~~~~~~\small{S^2 = \dfrac{1}{n-1} \sum_{i=1}^n (X_i - \overline{X})^2 }$$.
Then, the following are valid:

(a) \(~~~~\small{\overline{X}}\) and \(~\small{S^2}\) are independent parameters

(b) \(~~~~\small{\dfrac{(n-1)S^2}{\sigma^2}}~~ \) follows \(~\small{\chi^2(n-1),~~ }\)a chi-square distribution with (n-1) degrees of freedom.

\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) Theorem 4

Let \(\small{X_1, X_2, X_3,.....,X_n}\) be the random variables drawn from chi-square distributions \(\small{\chi^2(r_1), \chi^2(r_2), \chi^2(r_3),...,\chi^2(r_n)}\) respectively. If these random variables are independent, then their sum \(\small{Y = X_1 + X_2 + X_3+....+X_n }\) has a distribution that is \(\small{\chi^2(r_1 + r_2 + r_3 + ....+r_n) }\).

Thus, the sum of chi-square variables follows a chi-square distribution whose degrees of freedom is equal to the sum of the individual degrees of freedom.

\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) The effect of replacing population mean by the sample mean \(~~~~~~~~~~~~~~~~~~ \)
If \(\small{X_1,X_2,X_3,....X_i}\) are n random smaples from a normal distribution \(\small{N(\mu, \sigma)}\) and \(\small{\overline{X}}\) is the sample mean, then
$$ \small{U = \sum_{i=1}^n \dfrac{(X_i - \mu)^2}{\sigma^2}}~~follows~~\small{\chi^2(n) }$$ and $$ \small{W = \sum_{i=1}^n \dfrac{(X_i - \overline{X})^2}{\sigma^2}}~~follows~~\small{\chi^2(n-1) }$$
Thus, when the poulation mean \(\small{\mu}\) is replaced with the sample mean \(\small{X}\), one degree of freedom is reduced .

In general, if we estimate many independent parameters from the data, one degree of freedom per parameter estimated from data will be lost in chi-square variable.

\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) The concept of degrees of freedom \(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\)

The degrees of freedom of an estimated parameter is the number of independent data points used in arriving at the estimate. This in general is equal to the number of data points minus the number of parameters required to arrive at the estimated parameter in question.

For example we have n data points. In order to estimate the mean, we use all the n data points. Therefore, the degreees of freedom for mean is n. On the other hand, if we wish to estimate variance, we first need to compute the mean value and use it in the formula for variance. Therefore, the number of independent data points in the estimate of variance becomes (n-1). We thus say that the degrees of freedom for vairance is (n-1).



The Chi-square distribution table

The chi-square distribution has degrees of freedom as a parameter. For each value of degree of freedom r, separate distribution exists. The value of chi-square variable as a function of probability of getting a value above it (area under the curve above the variable value) is generally tabulated for various degrees of freedom. One such table can be accessed here.


In this table, for example, if chi-square value computed is 3.94 for 10 degrees of freedom, then the area of the curve for chi-square value greater than 3.94 is approximately equal to alpha = 0.05 (ie., alpha = 1 - 0.950)



R-scripts

R provides the following functions for computing the probability density and other quantities from Chisquare distribution : 


 dchisq(x, df) --------------> returns the chi-square probability density for a given x value and         
                                            degrees of freedom df
               
 pchisq(x, df) --------------> returns the cumulative probability from 0 upto x from a 
                                            chi-square distribution with df degrees of freedom.


 qchisq(x, df) ---------------> returns the  x value at which the cumulative probability is p from a 
                                               chi-square distribution with df degrees of freedom.

 rchisq(n, df) ---------------> returns n random numbers in the range [0 , infinity] from a                                                                                
                                            chi-square distribution with df degrees of freedom.



The R script below demonstrates the usage of the above mentioned functions:





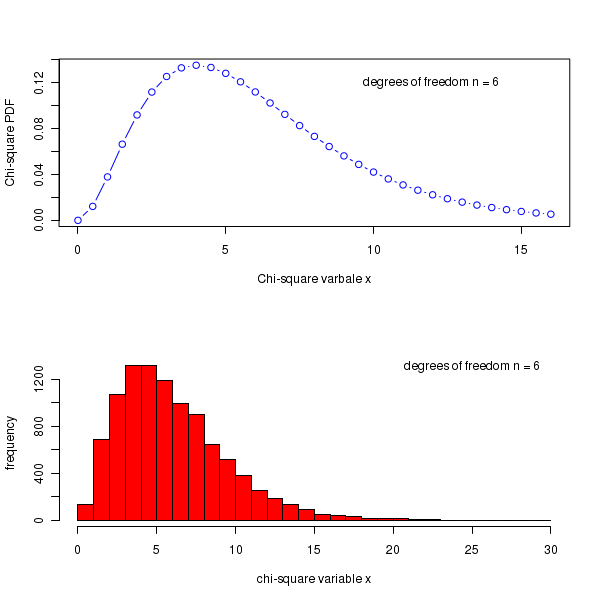
##### Using R library functions for Chi-square distribution
## Probability density for a given x, from a distribution with given degrees of freedom:
prob_dens = dchisq(x=6, df=5)
prob_dens = format(prob_dens, digits=4)
print(paste("Chi-square probability density for x=6, df=5 is = ", prob_dens))

## Cumulative probability upto x=6 for a Chi-square pdf with the given degrees of freedom.
cum_prob = pchisq(q=6, df=10)  ## function uses 'q' for x value
cum_prob = format(cum_prob, digits=4)
print(paste("chi-square cumulative probability upto x=6 for degrees of freedom 10 is  =  ", cum_prob))

## The value of variable x upto which the cumulative probability is p, for a 
## chi-square distribution with given degrees of freedom
x = qchisq(p = 0.85, df=6)
x = format(x, digits=4)
print(paste("value x at which cumulative probability is 0.85 for 6 degrees of freedom = ",x))

## Generate 5 random deviates from a chi-square distribution with degrees of freedom 10
print(rchisq(n=6, df=10))


## we will draw 2 graphs on the same plot

par(mfrow=c(2,1))

## Drawing a chi-square distribution pdf in x = 0 to 12, with df=6
x = seq(0,16, 0.5)
chisq_pdf = dchisq(x, df=6)
plot(x, chisq_pdf, col="blue", type="b", xlab="Chi-square varbale x", ylab="Chi-square PDF")
text(12.0, 0.12, "degrees of freedom n = 6 ")

## Plotting the frequency histogram of gamma random deviate for shape=4, scale=1
hist(rchisq(n=10000, df=6), breaks=30, col="red", xlab="chi-square variable x",                             ylab="frequency",main = " ")
text(25, 1300, "degrees of freedom n = 6")


Executing the above code prints the following lines and displays the following plots on the screen : 



[1] "Chi-square probability density for x=6, df=5 is =  0.0973"
[1] "chi-square cumulative probability upto x=6 for degrees of freedom 10 is  =   0.1847"
[1] "value x at which cumulative probability is 0.85 for 6 degrees of freedom =  9.446"
[1] 11.806898 10.434803  9.081138 13.650395 10.391160 17.583303